بسیاری عقیده دارند که مثلث حسابی پاسکال را باید مثلث حسابی خیام نامید و برخی پا را از این هم فراتر گذاشته اند و معتقد اند که دو جمله ای نیوتون را باید دوجمله ای خیام نامید . اندکی در این باره دقت کنیم.

همه کسانی که با جبر مقدماتی آشنایی دارند ،"دستور نیوتن" را درباره بسط دوجمله ای میشناسند. این دستور برای چند حالت خاص (وقتی n عددی درست و مثبت باشد) چنین است:

(a+b)0 = 1 (1)

(a+b)1 = a+b (1,1)

(a+b)2 = a2+2ab+b2 (1,2,1)

(a+b)3 = a3+3a2b+3ab2+b3 (1,3,3,1)

(a+b)4 = a4+4a3b2+6a2b2+4a2b3+b4 (1,4,6,4,1)

اعداد داخل پرانتزها، معرف ضریبهای عددی جمله ها در بسط دوجمله ای است.

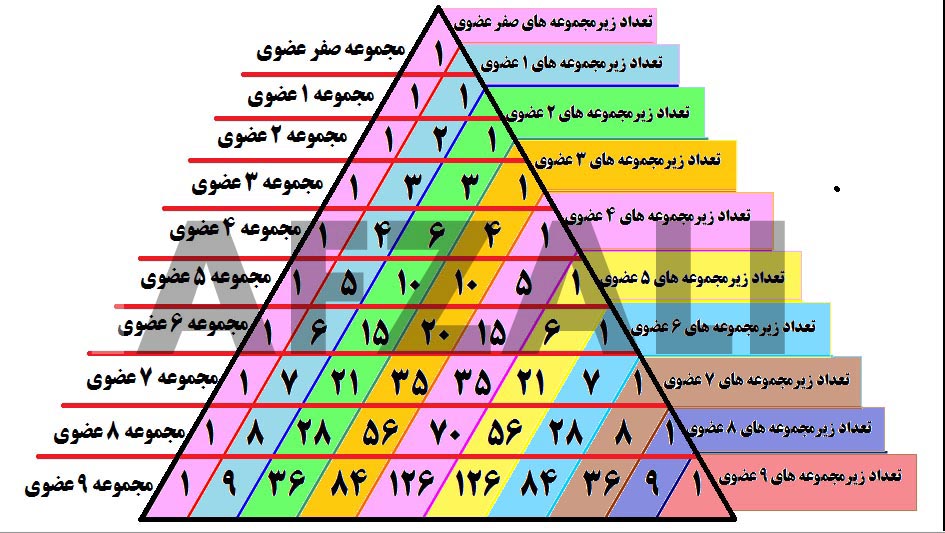
بلیز پاسکال (Blaise Pascal) فیلسوف و ریاضی دان فرانسوی که کم وبیش با نیوتون همزمان بود، برای تنظیم ضریبهای بسط دوجمله ای، مثلثی درست کرد که امروز به "مثلث حسابی پاسکال" مشهور است. طرح این مثلث برای نخستین بار در سال 1665 میلادی در "رساله مربوط به مثلث حسابی "چاپ شد.مثلث حسابی چنین است:

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

دراین مثلث از سطر سوم به بعد هر عددبرابر با مجموع اعداد بالا و سمت چپ آن در سطر قبل است و بنابراین میتوان آنرا تا هر جا که للازم باشدادامه داد. هرسطر این مثلث ضریبهای بسط دوجمله ای را در یکی از حالتها بدست میدهد بطوری که n همان شماره سطر باشد.

ضریبهای بسط دوجمله ای (برای توانهای درست و مثبت) حتا در سده دوم پیش از میلاد البته به صورت کم و بیش مبهم برای دانشمندان هندی روشن بوده است .باوجود این حق این است که دستور بسط دو جمله ای با نام نیوتن همراه باشد زیرا نیوتن آن را برای حالت کلی و وقتی n عددی کسری یا منفی باشد در سال 1676میلادی بکاربرد.که البته در این صورت به یک رشته بی پایان تبدیل میشود.

اما در باره مثلث حسابی وضریبهای بسط دوجمله ای در حالت طبیعی بودن n. از جمله، دستور بسط دو جمله ای را میتوان در "کتاب حساب مخفی" میخائیل شتیفل جبردان آلمانی (که در سال 1524 چاپ شد) پیدا کرد.

در سال 1948 میلادی،پاول لیوکی آلمانی،مورخ ریاضیات،وجود دستور نیوتن را برای توانهای طبیعی ،دز کتاب "مفتاح الحساب"(1427 میلادی) غیاث الدین جمشید کاشانی کشف کرد. بعدها س.آ.احمدوف ،مورخ ریاضیات و اهل تاشکند، دستور نیوتون وقانون تشکیل ضریبهای بسط دوجمله ای را،در یکی از رساله های نصر الدین توسی،ریاضیدان بزرگ سده سیزدهم میلادی ،کشف کرد (این رساله توسی درباره محاسبه بحث میکند). چه جمشید کاشانی وچه نصرالدین توسی ،این قاعده را ضمن بررسی قانون های مربوط به ریشه گرفتن از عددها آورده اند.

همچنین براساس آگاهی هایی که داریم حکیم عمر خیام رساله ای داشته که خود رساله تاکنون پیدا نشده ولی از نام آن "درستی شیوه های هندی در جذر وکعب "اطلاع داریم ،کهدر آن به تعمیم قانونهای هندی درباره ریشه دوم و سوم ،برای هر ریشه دلخواه پرداخته.لذا خیام از "دستور نیوتن" اطلاع داشته.

اما بنا به اسناد تاریخی معتبر قانونهای مربوط به ضریبهای بسط دوجمله ای وطرح مثلث حسابی تا سده دهم میلادی(برابر چهارم هجری) جلو میرود و به کرجی (ابوبکر محمد بن حسن حاسب کرجی ریاضیدان سده ده و یازده میلادی) پایان می پذیرد .بنابراین حتی" مثلث حسابی پاسکال" را هم از نظر تاریخی نمیتوان "مثلث حسابی خیام " نامید.

نظرات شما عزیزان:

نام :

آدرس ایمیل:

وب سایت/بلاگ :

متن پیام:

نظر خصوصی

 کد را وارد نمایید:

 

 

 

عکس شما

آپلود عکس دلخواه: